Welcome to my site where I document my research on the Collatz Conjecture.
The Collatz Conjecture is a conjecture in mathematics that states that for any positive integer n, the following process will eventually reach 1:
For example, starting with n = 6, we get the following sequence:
6, 3, 10, 5, 16, 8, 4, 2, 1
The Mini-Collatz Conjecture is a variant with the following simplified rules:
This smaller problem is much easier to solve than the original Collatz Conjecture.
If you try a few examples, it becomes immediately obvious that the division by 2 quickly dominates the addition of 1.
The proof that this one always goes to 1 is as follows:
Notice that in the scenario when n is odd we add 1. This then makes the number even again meaning the next step will always be a division by 2. We can therefore define a new function F(n) where:
This is similar to the original system (the first case is the same), but we are double-stepping the odd case and doing the next divison by 2 immediately.
But notice that F is just: F(n) = ⌈n/2⌉. This clearly shows the F monotonically decreases and therefore must eventually reach 1.
There is a bit more subtlety to a precise proof but the edge cases are trivial to clean up.
This gives some nice intuition as to why the original Collatz Conjecture is so difficult. There, it is less clear which wins out in the long term: the division by two or the multiplication by three.
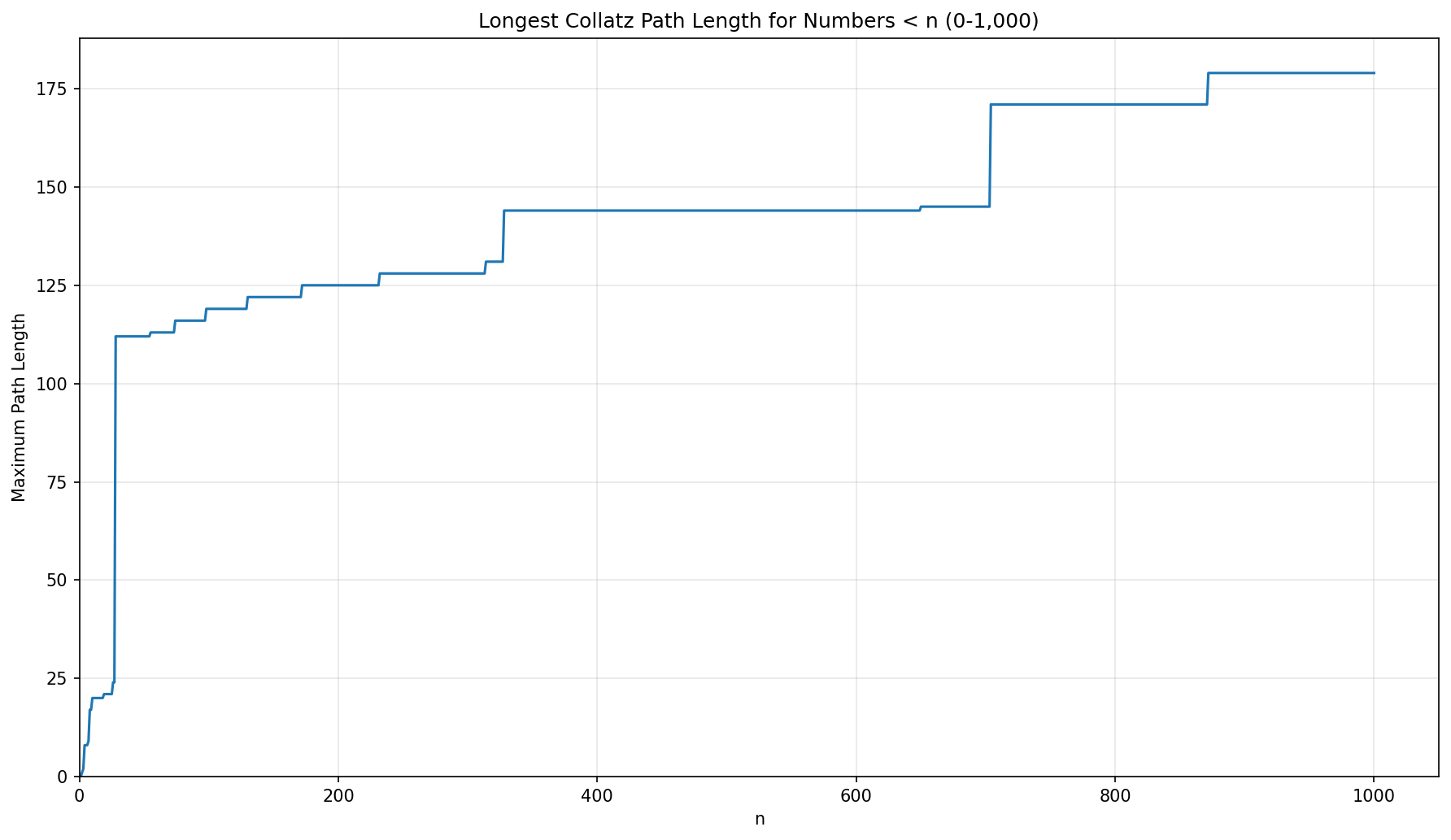
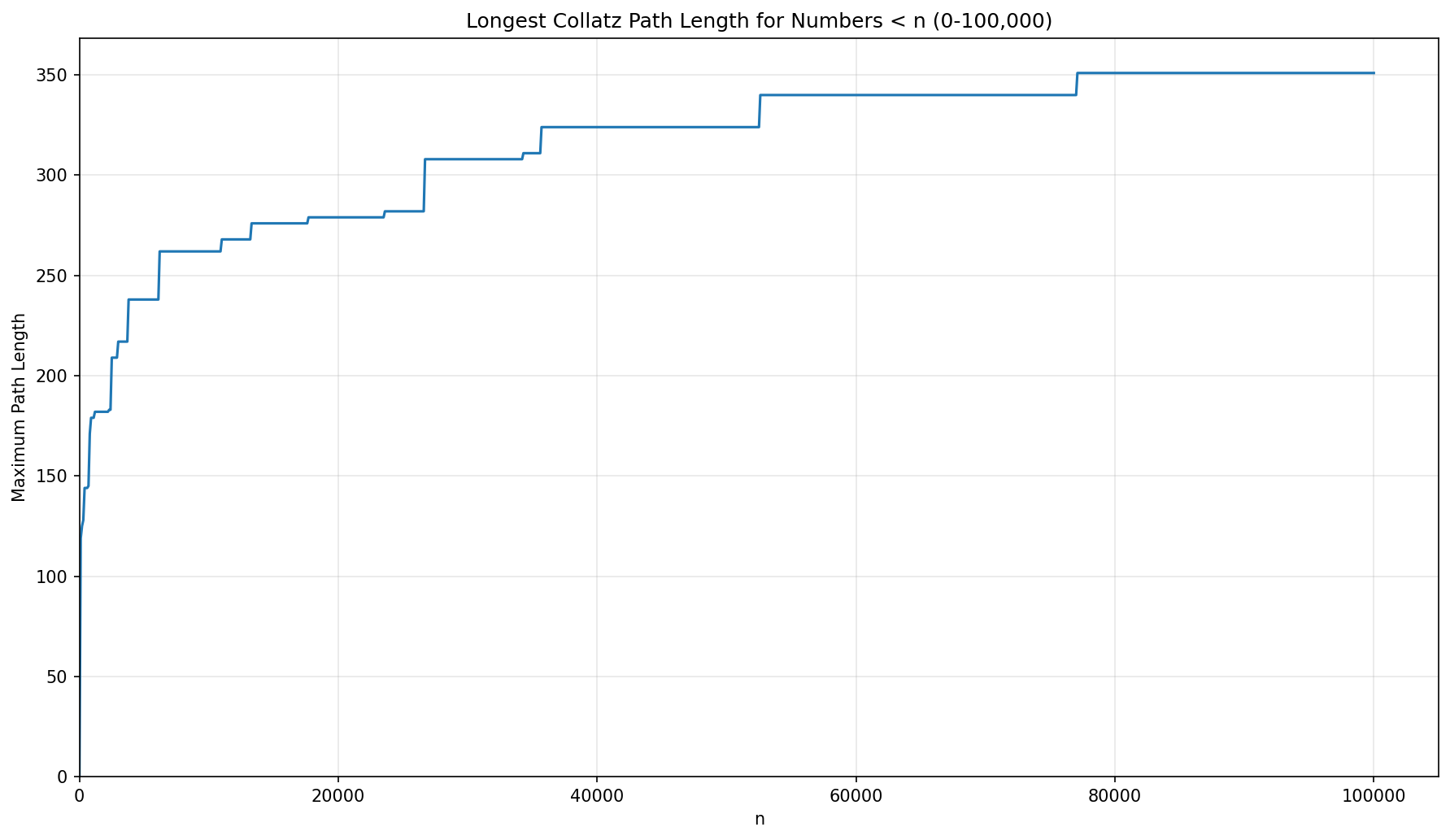
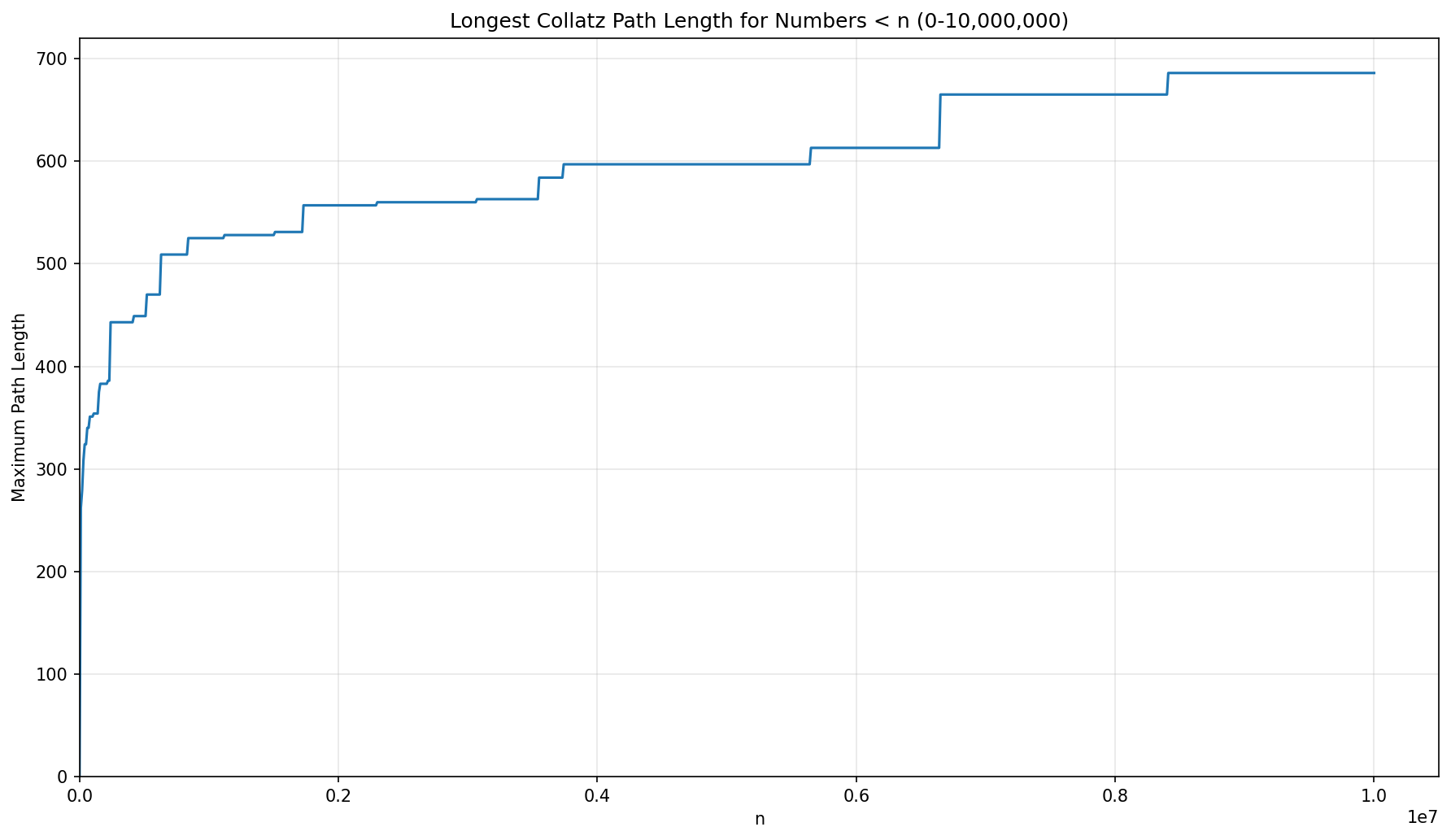
The following 3 graphs show the maximum path length for the Collatz Conjecture for numbers less than 1,000, 100,000, and 10,000,000 respectively.